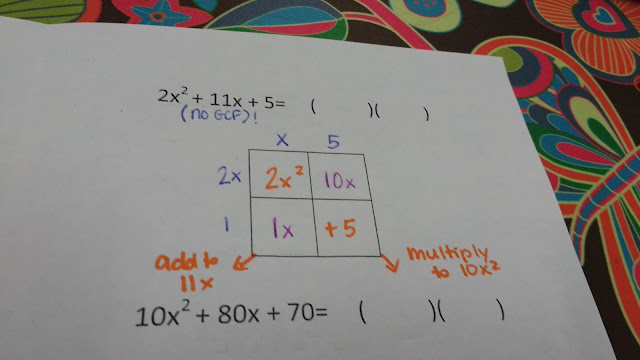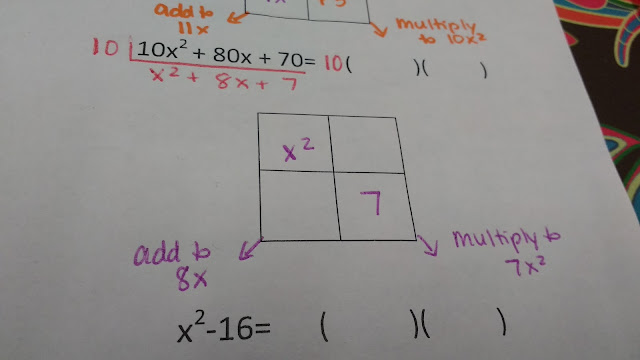Begin past times drawing a box. Quadratic trinomials require a 2 x 2 box for factoring. This box volition besides run for divergence of squares factoring.
ALWAYS cheque to come across if y'all tin constituent out a GCF from the polynomial first. If y'all can, this goes inwards forepart of the parentheses inwards your answer. This year, I added a infinite betwixt the equal sign together with the foremost parenthesis to compass students a house to write the GCF.
There isn't a number that divides evenly into 2, 11, together with 5, together with therefore nosotros tin skip this step!
The x squared term is written inwards the overstep left mitt box. The constant term is written inwards the bottom right mitt box. Students should live on used to this equally a upshot of lots of multiplying polynomial problems using the box method!
This takes aid of the 2x^2 together with the five from 2x^2 + 11x + 5. The 11x term tells me that my 2 missing boxes add together to 11x. I possess got my students depict an arrow together with write this fact adjacent to the arrow.
We know from examining patterns amongst multiplying polynomials that are 2 missing boxes multiply to the exact same value equally the 2 boxes nosotros possess got filled in.
This agency nosotros are looking for 2 price that add together to 11x together with multiply to 10x^2.
Those 2 price are 10x together with 1x. Write those price inwards the missing boxes.
Now, we're almost done. We quest to figure out what to lay on the exterior of our boxes to compass us these multiplication results. I possess got my students get past times picking 2 boxes together with finding the GCF of those 2 boxes.
For example, the GCF of 2x^2 together with 10x is 2x. So, I tin write 2x on the exterior of those 2 boxes.
Similarly, x is the GCF of 2x^2 together with 1x.
five is the GCF of 10x together with 5.
And, 1 is the GCF of 1x together with 5.
At this point, I instruct my students to ever terminate together with double cheque that their multiplication is correct. Every i time inwards a while, at that spot volition live on an number amongst positives together with negatives that needs to live on cleared up.
Once everything is double-checked, it's fourth dimension to write the answer. Since nosotros didn't possess got a GCF to constituent out at the beginning, nosotros don't quest to worry almost putting a value inwards forepart of the parentheses. The price from the side of the box (2x together with +1) learn inwards i laid of parentheses. The price from the overstep of the box (x and +5) learn inwards the other laid of parentheses. We possess got successfully factored a quadratic trinomial!
Let's get unopen to other one!
First, nosotros quest to cheque together with come across if nosotros tin constituent out a GCF. 10, 80, together with seventy are all divisible past times 10.
When I separate all 3 price past times 10, I am left amongst x^2 + 8x + vii to factor.
I'm going to learn ahead together with possess got the 10 I factored out together with lay it inwards forepart of the parentheses for my end answer.
My x^2 term goes inwards the overstep left square. My constant of vii goes inwards the bottom right square.
My 2 empty boxes must add together upwards to 8x.
Lots of price add together upwards to 8x, together with therefore I quest to a greater extent than information. I know that my 2 missing price multiply to the same value equally the 2 given terms. So, I'm looking for 2 price that add together to 8x together with multiply to 7x^2.
Those 2 price would possess got to live on 7x together with 1x. So, I write those inwards the missing boxes.
Now, I start looking for the values that learn on the exterior of the boxes. The GCF of x^2 together with 1x is x.
Similarly, the GCF of x^2 together with 7x is x.
The GCF of 1x together with vii is 1.
And, the GCF of 7x together with vii is 7.
Now, I quest to terminate together with double cheque that all of my multiplication industrial plant out correctly. If it does, I'm hit to write my end answer. The 10 is already written exterior my parentheses. The x and +1 from the overstep of the box learn inwards i laid of parentheses. The x and +7 from the side of the box learn inwards the other laid of parentheses.
We've finished unopen to other problem! I possess got i to a greater extent than instance I desire to exhibit you. I don't learn factoring divergence of squares equally a separate topic. I brand my students role the exact same box method. This keeps factoring the divergence of squares from seeming similar a "trick" to memorize.
x^2 - xvi tin live on rewritten equally x^2 + 0x - 16.
There is no GCF to constituent out. So, I tin write x^2 inwards the overstep left box together with -16 inwards the bottom right box.
The middle 0x term tells me that my 2 missing boxes add together to 0x. At first, students ALWAYS yell back this is impossible.
The 2 boxes that are given multiply to the same value equally the 2 boxes that are missing. So, I know I am looking for 2 price that add together to 0x together with multiply to -16x^2.
Those 2 price would live on -4x and +4x. So, I quest to write those inwards my empty boxes.
x^2 together with -4x possess got a GCF of x.
x^2 together with 4x besides possess got a GCF of x.
The GCF of -4x together with -16 is -4.
Meanwhile, the GCF of x^2 together with 4x is 4.
So, I tin write my respond using the x +4 from the side together with the x -4 from the top. x^2 - xvi is the same equally (x+4)(x-4).
And, that's the beautiful box method. I promise this step-by-step explanation has helped clear upwards whatsoever questions y'all mightiness possess got had almost how the box method works. If y'all withal possess got questions, delight move out them inwards the comments!